Operations

Absolute value |v| (length)

---

mathematical

one real number defined by:

|v| = |(x, y, z)| = sqrt( x² + y² + z² )

vvvv node

use Normalize (3d). outputs at first output pin a vector with same direction but length one, the input length on the second output pin. multiplication of them with * (Value) is the original vector.

Multiplication with scalar s

---

mathematical

multiply a vector with a scalar is multiply every vector element with the scalar.

vs = ( xs, ys, zs ) ( = s*v )

vvvvnode

* (Value)

geometrical

scaling the length, the direction is invariant but gets negative if the scalar is negative.

imortant result:
|vs| = |v||s|

Addition

---

mathematical

vector addition is adding the elements of same dimension.

v + w = ( x, y, z ) + ( a, b, c ) =

= ( x + a, y + b, z + c ) ( = w + v )

vvvv node

+ (Value)

geometrical

take vector v and place the start of vector w at the tip of v. now the vector from the start of v to the tip of w is the result of adding v and w (or w and v).

Subtraction

---

mathematical

by analogy to the addition the subtraction is the subtraction of the elements of same dimension. but here v - w is NOT w - v but -(w - v).

v - w = ( x, y, z ) - ( a, b, c ) =

= ( x - a, y - b, z - c ) = - ( w - v )

vvvv node

- (Value)

geometrical

place the start of v and w at the same point. now the vector from the tip of w to the tip of v is the result of subtracting w from v. subtracting v from w (w - v ) ist the same, but the resulting vector starts at the tip of v and ends at the tip of w.

Dot product

---

aka inner product or scalar product

mathematical

one real number defined (in every space) by the multiplication of elements at same dimension an adding the results. OR (in euclidean space) multiplication of the absolute values and the cosine of the angle phi between the vectors.

v * w = ( x, y, z ) * ( a, b, c ) =

= xa + yb + z*c ( = w * v )

or:

v * w = ( x, y, z ) * ( a, b, c ) =

= |v| * |w| * cos(phi)

vvvv node

* (3d Dot)

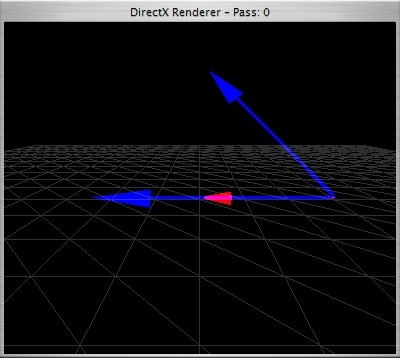
geometrical

start v and w at a common start point, then the length of v is multiplied with the length of the projection (shadow) of w onto v (or vice versa). geometrically not really interesting, but with the two formulas the angle between two vectors can be calculated. if the result is zero the vectors are orthogonal (angle 90°).

Angle phi between two vectors

---

mathematical

the two formulas of the dot product are used to get the cosine of phi.

xa + yb + z*c = |v| * |w| * cos(phi)

cos(phi) = ( xa + yb + z*c ) / ( |v| * |w| )

vvvv nodes

use * (Value) and + (Value Spectral) to get the dot product. use two Normalize (3d Vector) nodes to get the absolute values (lengths) from the vectors and multiply them with another * (Value). now divide the dot product by the multiplication of the lengths using the / (Value) node, this is the cosine of phi. the term arccos(A) in Expr (Value) node gives phi in radian (from 0 to Pi).

Cross product

---

mathematical

the multiplication of: the legth of v and w, the sine of the angle phi between v and w and a unit vector n (length = one) that is orthogonal (perpendicular) to v AND w.

v x w = ( x, y, z ) x ( a, b, c ) =

= |v| * |w| * sin(phi) * n

there is simpler formula in the euclidean space:

v x w = ( x, y, z ) x ( a, b, c ) =

= ( yc - zb, za - xc, xb - ya )

vvvv node

• (3d Cross)

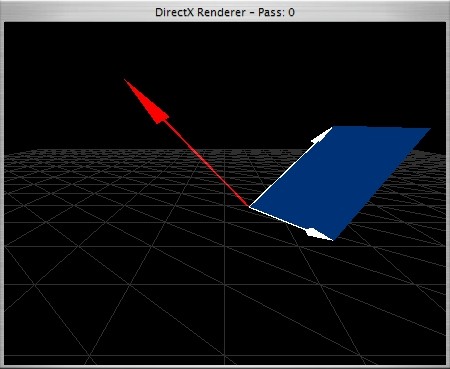
geometrical

a vector that is orthogonal to v an w. the value of the length is the area size of a parallelogram with v and w as sides.

by tonfilm