Function Printing

There are various possibilities to alter the vertex positions by mathematical functions.

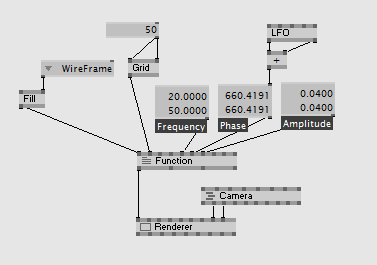
For the following examples we use a Grid (EX9.Geometry) as input. Set the resolution to about 50x50.

f(x, y) = z

Create a new z coordinate by x and y. Using the MrWiggle example we could write:

float2 Frequency = 10;  
float2 Phase = 0;  
float2 Amplitude = 0.01;  

vs2ps VS(  
    float4 PosO  : POSITION,
    float4 TexCd : TEXCOORD0)
{  
    //declare output struct
    vs2ps Out;
    
    //calculate two waves
    float2 wave = sin(PosO.xy * Frequency + Phase) * Amplitude;
    
    //set z coordinate
    PosO.z = wave.x + wave.y;

    //transform position
    Out.Pos = mul(PosO, tWVP);
    
    //transform texturecoordinates
    Out.TexCd = mul(TexCd, tTex);

    return Out;
}  

using a patch like:

f(u, v) = xyz

Another common type is to calculate a completely new position from the xy coordinates of the grid. This is often called parametric surfaces, where the xy input parameters are called uv.

for example a cone:

x = v*cos(u)  
y = v*sin(u)  
z = v  

can be written as a function:

float3 Cone(float2 uv)  
{  
	float u = uv.x;
	float v = uv.y;
    
	float3 newPos;
	newPos.x = v * cos(u);
	newPos.y = v * sin(u);
	newPos.z = v;
	
	return newPos;
}  

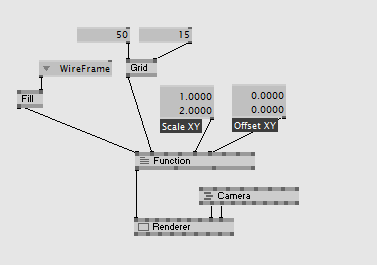
It might be handy to scale u by two pi to get a full cycle in the range 0..1, as well as have a general offset and scale for the input parameters. The vertex shader could then look like:

1. define twopi 6.28318531

float2 Scale = 1;  
float2 Offset = 0;  

float3 Cone(float2 uv)  
{  

 	uv *= Scale;
 	uv += Offset;
 
	float u = uv.x * twopi;
	float v = uv.y;
    
	float3 newPos;
	newPos.x = v * cos(u);
	newPos.y = v * sin(u);
	newPos.z = v;
	
	return newPos;
}  

vs2ps VS(  
    float4 PosO  : POSITION,
    float4 TexCd : TEXCOORD0)
{  
    //declare output struct
    vs2ps Out;
    
    //set new position
    PosO.xyz = Cone(PosO.xy);

    //transform position
    Out.Pos = mul(PosO, tWVP);
    
    //transform texturecoordinates
    Out.TexCd = mul(TexCd, tTex);

    return Out;
}  

And the patch:

Next: Vertex Data
Back: Mr. Wiggle
TOC: ((Tutorial - Of Effects and Shaders|Of Effects and Shaders))